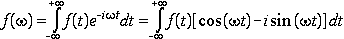
Immagina f() come la sovrapposizione di f(t) con una forma d'onda di frequenza.

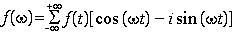
E' più facile da rappresentare considerando solo la parte reale f().

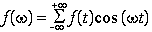
Consideriamo ora la funzione del tempo, f( t ) = cos( 4t ) + cos( 9t ).

Per capire la FT, esaminiamo il prodotto di f(t) con il cos(wt) per w valori tra 1 e 10, e poi la somma dei valori di questo prodotto tra 1 e 10 secondi. La somma esaminerà solo per valori di tempo tra 0 e 10 secondi.

w=1

w=2

w=3

w=4

w=5

w=6

w=7

w=8

w=9

w=10

f(w)

in pratica possiamo vedere che moltiplicando punto per punto la nostra forma d'onda con una funzione arbitraria ( cos(t) ) di frequenza nota (f) otterremo ogni volta una nuova forma d'onda della quale eseguiremo la sommatoria algebrica di ciascun punto: il risultato di questa sommatoria (che sarà un unico numero ovviamente es.:120) rappresenterà l'ampiezza della frequenza contenuta nella funzione da "trasformare" f(t).

Copyright © 1996-2000 J.P. Hornak.
All Rights Reserved.